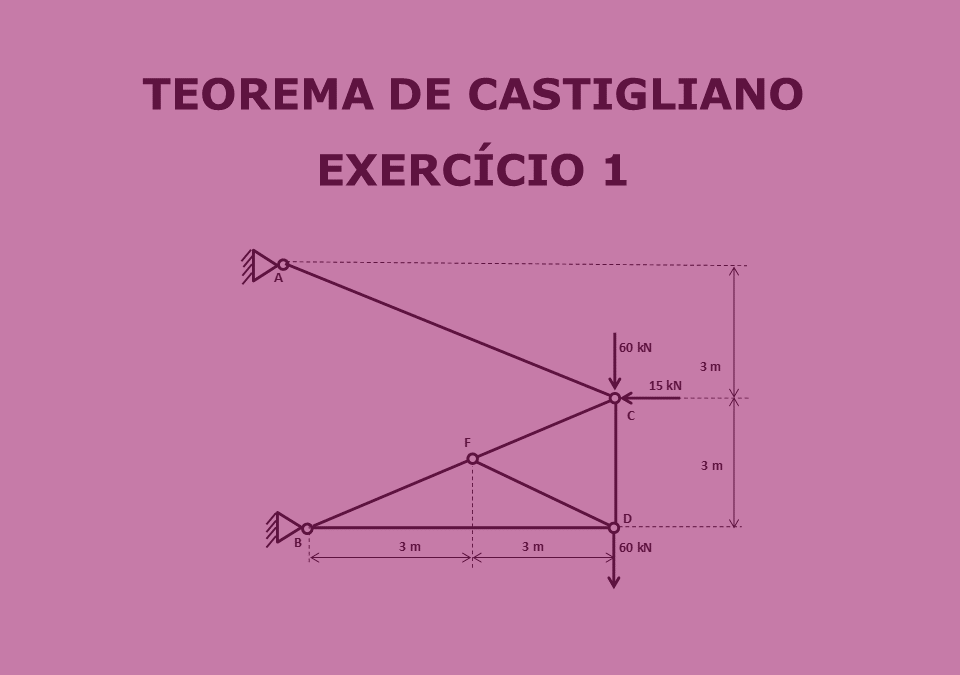
Questão Proposta:
A figura acima representa uma treliça como modelo estrutural de uma construção metálica. Para avaliar a rigidez desta estrutura, pede-se:
a) Os valores dos esforços internos em cada barra, indicando se a barra está sendo tracionada ou comprimida;
b) O deslocamento vertical do nó D, devido à ação das forças aplicadas na estrutura.
Dado: EA = 850 000 kN
Para resolver este exercício, precisamos, inicialmente, determinar as reações dos apoios. Posteriormente aplicaremos o método dos nós para determinar cada esforço interno na barra. Então, vamos adotar os seguintes sentidos das reações:
Passo 1) Reações dos apoios

Para determinar as reações dos apoios, vamos adotar os sentidos positivos, ou seja, horizontal para a direita e vertical para cima. Se nossas reações derem negativas, inverteremos os sentidos das mesmas. Para aplicar a somatória dos momentos, vamos adotar o sentido horário negativo. Logo, nosso sistema de referência ficou assim:
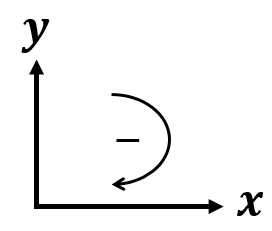
Vamos aplicar a somatória de momento no apoio que tem mais reações, sendo assim, aplicaremos a somatória no apoio B! Mas vejam que temos duas parcelas do RA, uma na horizontal e outra na vertical. Vamos ilustrá-las com um ângulo conhecido.
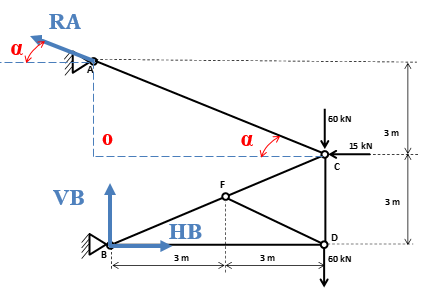
Com o ângulo α localizado na força RA, conseguimos decompô-la e descrever suas componentes em função deste ângulo. Lembrando que a componente horizontal está “com o ângulo α”, portanto cosseno α e a vertical está “sem o ângulo α”, portanto senoα
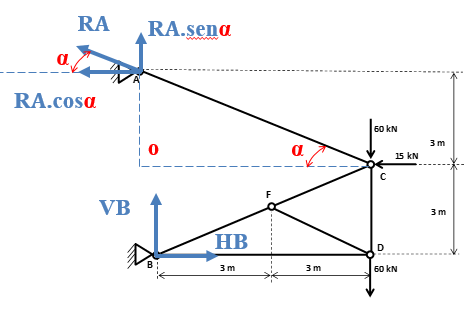
Para facilitar os nossos cálculos, vamos determinar o seno e cosseno do ângulo α. Antes devemos calcular o valor da hipotenusa e posteriormente aplicar as relações trigonométricas. Chamaremos a hipotenusa do triângulo AOC de z. Então temos:
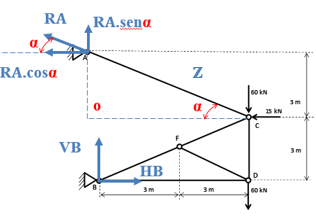

Após realizar a decomposição da força RA, podemos aplicar a somatória de momento no apoio B. Vale ressaltar que a componente RA.sen α não produz momento em relação ao Apoio B, pois esta componente não tem um “braço” perpendicular ao apoio B. Para tanto, apenas a componente horizontal produz momento em relação ao apoio B! Sendo assim, temos:

Vamos, agora, aplicar a somatória de forças verticais para encontrar a reação VB:

Vamos, agora, aplicar a somatória de forças horizontais para encontrar a reação HB:

Passo 2) Análise dos nós
Com as reações dos apoios determinadas, vamos analisar os nós separadamente. Iniciaremos a análise pelo nó A. Adotaremos todas as forças “saindo do nó” e “indo” em direção a barra. Isso significa que estamos supondo tração no nó, sendo assim, se nosso esforço resultar positivo, o esforço é de tração, caso contrário é compressão. Vamos ilustrar a situação:
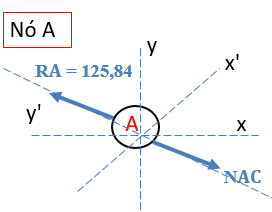
Para não termos que decompor as forças em relação aos eixos x e y, vamos utilizar o eixo y’ para somatórias das forças.

Vamos, então, analisar o nó C.
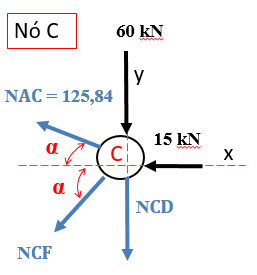
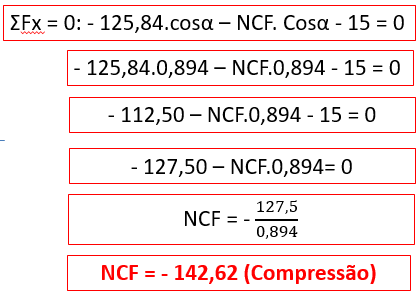
Com a força NCF determinada, podemos aplicar a somatória de forças em relação ao eixo y para determinar a força NCD

Vamos, agora, analisar o nó D.
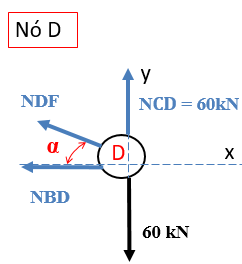
Neste nó, nós temos que colocar o ângulo α com a força inclinada, assim conseguiremos trabalhar com suas componentes. Vamos, então, aplicar a somatória de forças em relação ao eixo y.
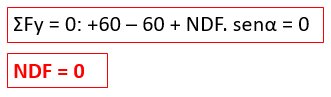
Com a força NDF = 0, podemos aplicar a somatória de forças em relação ao eixo x para determinar a força NBD.

Vamos, agora, analisar o nó F.
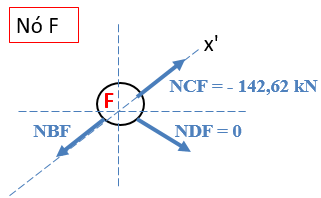
Como a força NDF = 0, podemos aplicar a somatória de forças em relação ao eixo x’ para determinar a força NBF.

Com todas as forças determinadas, podemos dar a resposta solicitada através de uma tabela autoexplicativa.
RESPOSTA
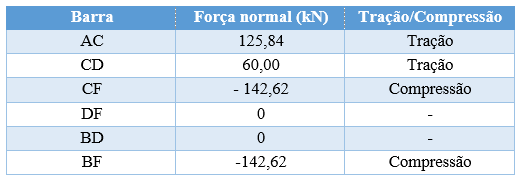
No item b, ele pede para calcularmos o deslocamento vertical que ocorre no nó D. Para determinar esse deslocamento precisamos encontrar as reações internas causadas por uma força unitária na direção e sentido do deslocamento solicitado. Vamos analisar a fórmula.

Ni = Forças normais nas barras com os carregamentos reais;
Nxi = Forças normais nas barras com um carregamento unitário na direção e sentido do deslocamento.
li = Comprimento da barra
E = Módulo de Elasticidade do material
A = Área da seção transversal.
Entendido o que é cada item da fórmula, vamos em busca das forças normais nas barras com um carregamento unitário na direção e sentido do deslocamento. Analisemos a imagem abaixo:
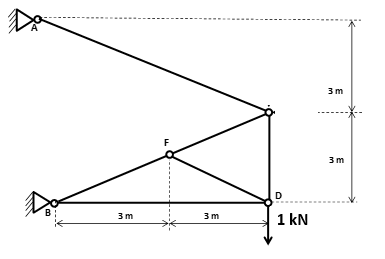
Como nos foi pedido o deslocamento vertical, devemos colocar uma força unitária na direção vertical no ponto solicitado. O sentido é indiferente, podemos adotar para cima ou para baixo! Se, no resultado, o sinal der negativo, significa que o deslocamento está no sentido contrário ao adotado. Vamos adotar os sentidos das novas reações da seguinte maneira:
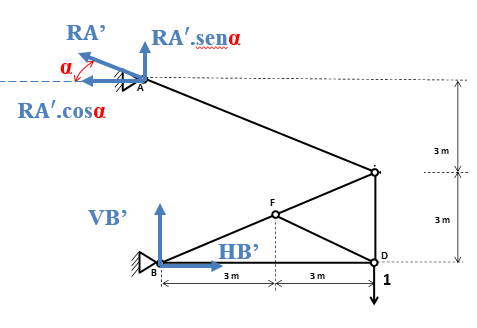
Para diferenciar das reações iniciais, vamos chamar as novas reações de RA’, VB’ e HB’, e colocaremos a “linha” em todas as reações internas, isso nos ajudará a diferenciar das primeiras reações encontradas. Vamos repetir os passos anteriores! Somaremos momento no apoio B para encontrar a reação RA’.
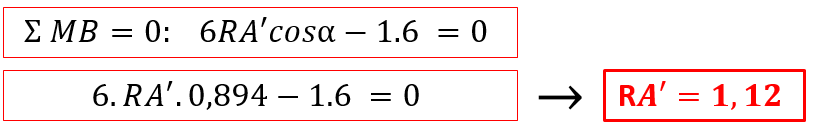
Com RA’ determinado, vamos aplicar a somatória de forças na vertical para determinar o VB’ e posteriormente a somatória de forças na horizontal para determinar o HB’.

Não colocaremos unidade nas forças, pois elas são “fictícias”, são produzidas por um valor unitário e adimensional. Vamos, então, repetir a análise dos nós na mesma sequência que fizemos para a estrutura real.
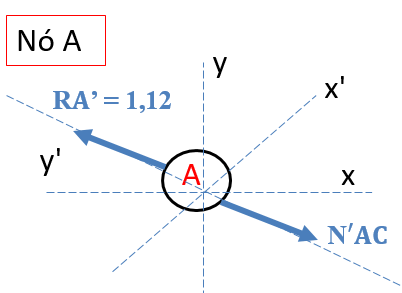
Novamente, vamos somar forças em relação ao eixo y’.
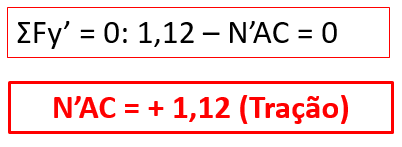
Vamos, agora, analisar o nó C:
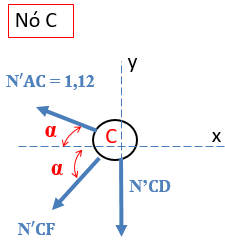
Vamos iniciar somando forças em X, assim determinaremos o valor de N’CF

Agora somaremos força em Y, assim determinaremos os valores de N’CD

Vamos, agora, analisar o nó D:
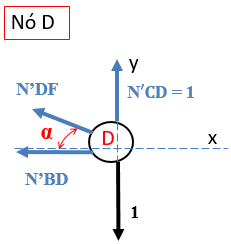
Visivelmente a força N’CD se anula com a força fictícia de valor 1, assim o resultado da N’DF é zero. Para tanto, N’BD também é zero. Vamos as contas:

Por fim, vamos analisar o nó F:
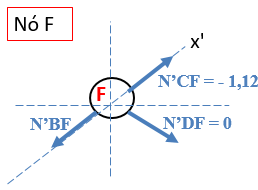
Somando força no eixo x’, temos:
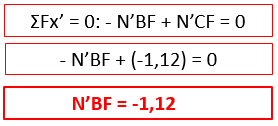
Vamos montar uma tabela ilustrando todas as forças fictícias encontradas.
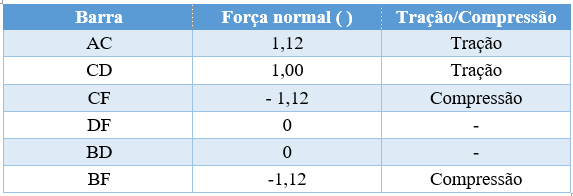
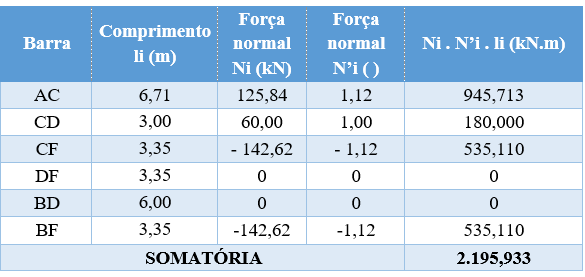
Vamos montar uma tabela ilustrando todas as forças encontradas (N e N’), bem como o comprimento das respectivas barras. No final, faremos a soma do produto entre esses elementos.
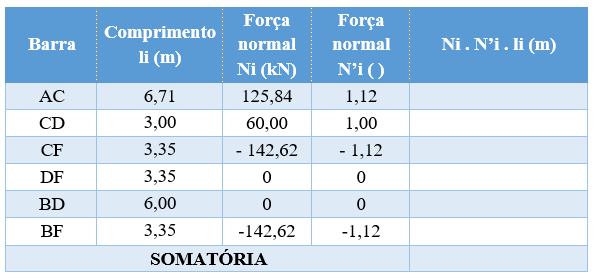
Após colocar na tabela, todos os valore conhecidos, vamos multiplicar os três valores de cada barra para preencher a última coluna.
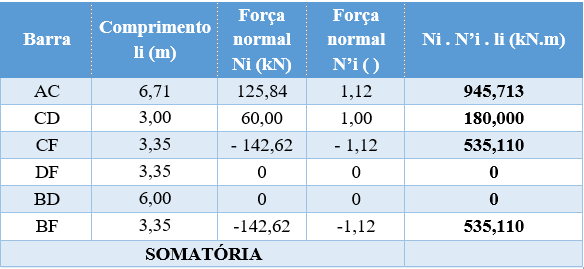
Por fim, vamos somar a última coluna.
Relembrando, a fórmula do deslocamento é descrita por:

Note que já calculamos o denominador! É exatamente a nossa soma na tabela a cima.
O E.A foi fornecido e seu valor é: EA = 850 000 kN
Aplicando a Fórmula, temos:
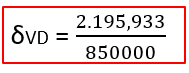
O resultado do nosso deslocamento vertical em D, em metros é:
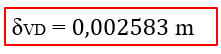
Como o deslocamento é muito pequeno, vamos deixa-lo na ordem de milímetros, resultando em:
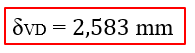
Até a próxima galera! Se tiverem dúvidas em alguma passagem do exercício, deixe – as nos comentários.
A sua dúvida pode ser a mesma de outro aluno!
Abraços!