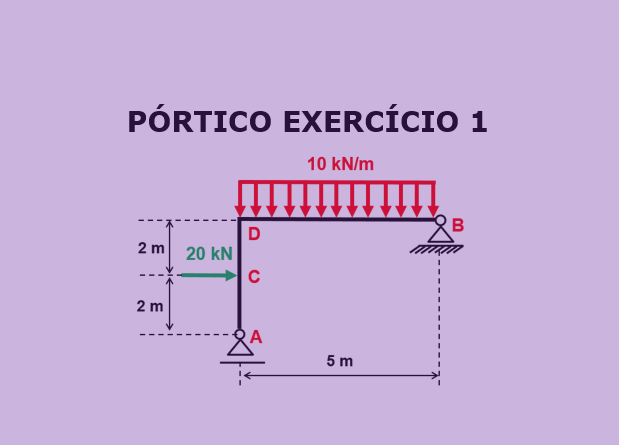
Questão Proposta:
A figura acima representa um pórtico plano constituído em concreto armado. Pada esse pórtico, determine:
a) As reações dos apoios.
b) Os diagramas dos esforços internos solicitantes.
Observação: Utilize duas casas decimais.
Como pedido no exercício, vamos determinar as reações dos apoios. Para tanto, vamos adotar a direção e sentido das reações conforme a figura abaixo:
Passo 1) Direção e sentido das reações.
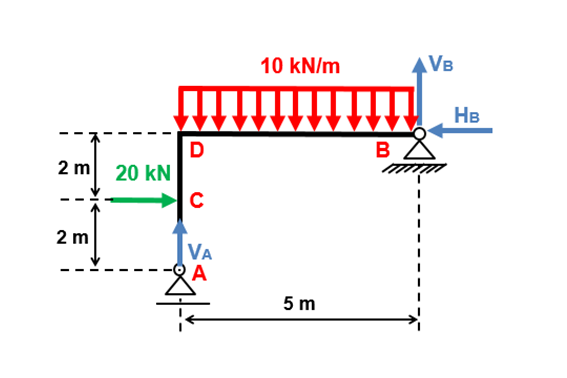
Para determinar as reações dos apoios, vamos adotar que horizontal para a direita e vertical para cima são positivos. Se nossas reações derem negativas, inverteremos os sentidos das mesmas. Para aplicar a somatória dos momentos, vamos adotar o sentido horário negativo. Logo, nosso sistema de referência ficou assim:
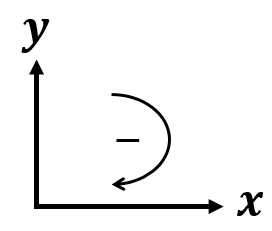
Vamos aplicar a somatória de momento no apoio que tem mais reações, sendo assim, aplicaremos a somatória no apoio B! Logo, encontraremos o valor de VA.
ΣMB = 0: – VA . 5 – 20 . 2 – 10 . 5 . 2,5 = 0 -> VA = 33 kN
ΣV = 0: + 33 – 10.5 + VB = 0 -> VB = 17 kN
ΣH = 0 -> + 20 – HB = 0 -> HB = 20 kN
Como todas as reações deram positivas, significa que adotamos o sentido correto. Portanto, o nosso pórtico tem essa cara:
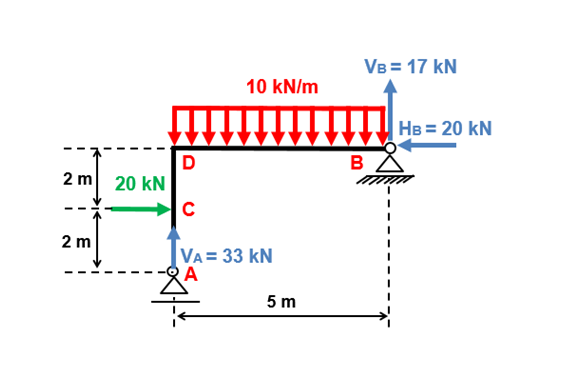
Temos, então, a resposta do item A.
Passo 2) Análise dos trechos
Com as reações dos apoios determinadas, vamos analisar trecho a trecho para fazer o diagrama de esforços internos solicitantes. Iniciaremos a análise pelo trecho AC .
A sacada é olhar o que a força faz com o corte.
Aqui você deve se perguntar: “Essa força traciona ou comprime o meu corte?
Se tracionar, é positiva! Se comprimir, é negativa!
Vamos ilustrar a situação:
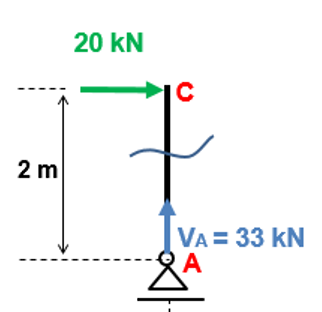
NAC = – 33 kN (Comprime o corte)
Vamos analisar o que está acontecendo aqui. Primeiro, de A até C, nós só temos VA, certo?
VA está tendendo a tracionar ou comprimir o corte que fizemos nesse trecho?
Se você por uma caneta no lugar de VA e movê-la até o corte, verá que ela comprimirá. E se ela comprime o corte, significa que qualquer corte que fizermos nesse trecho, será comprimido por essa força.
Logo, temos uma força de compreção ao longo do trecho AC. E se ela comprime, seu sinal é negativo!
Vamos, então, analisar o trecho CD.
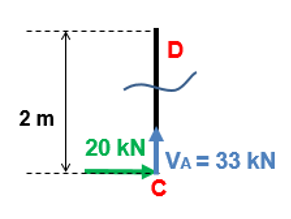
NCD = – 33 kN (Comprime o corte)
VCD = – 20 kN (gira no sentido anti-horário)
MCD = 20×2 = 40 kN.m (Tracionando do lado esquerdo da barra)
Veja que agora temos VA e a força de 20 kN. Isso, porque devemos trazer todas as forças do trecho AC para o ponto C. Agora, a pergunta que devemos nos fazer, é:
1) A força VA traciona ou comprime o corte?
2) Essa força de 20 kN, tende a girar a viga no sentido horário ou anti-horário? Ela flete a barra?
As respostas para essas perguntas são:
1) VA comprime o corte! Lembra da dica da caneta? use a mesma teoria e verá que o corte será comprimido. Logo todo o trecho CD será comprimido por VA.
2) A força de 20 kN tende a girar a barra no sentido anti-horário. Portanto ela será uma cortante negativa.
Essa força também Flete a nossa barra! Então temos que imaginar qual sentido está sendo tracionado! Note que nesse caso ela está tracionando o lado esquerdo do trecho CD.
E AGORA, QUAL TRECHO EU ANALISO? DB OU BD?

Eu super recomendo você analisar o de B para D, assim não terá que carregar o momento produzido pela força de 20 kN, e acredite, você pode perder o exercício completamente se esquecer de fazer isso!
Então vamos cortar de B para D.
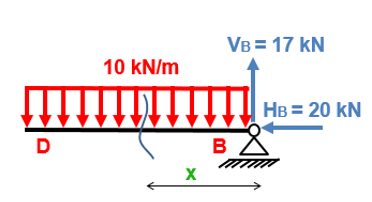
Note que a única força normal que temos nesse trecho é a força HB. E ela comprime o trecho BD.
NBD = – 20 kN (Comprime o corte)
Já a força VB tende a girar a barra no sentido anti horário, portanto ela é negativa. Contudo, nós temos o carregamento de 10 kN/m que tende a girar a viga no sentido horário, portanto ele será positivo. Lembrando que ele varia em função de X, logo temos:
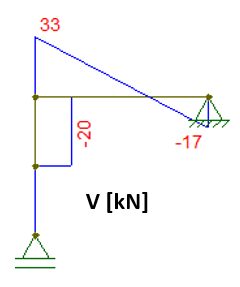
VBD = – 17 + 10x
Em x = 0 (Ponto B): VBD = – 17 + 10.0 -> VBD = – 17 kN
Em x = 5 (Ponto D): VBD = – 17 + 10.5 -> VBD = + 33 kN
Como a cortante passou pelo zero, devemos calcular o xmax.
Para V = 0: 0 = – 17 + 10x -> Xmax = 1,70 m
Ou, pela fórmula pronta:
Xmax = V/w -> Xmax = 17/10 -> Xmax = 1,70 m
(Nesse ponto o momento é máximo)
Vamos , então, calcular o momento nesse trecho. As forças que produzem momento em relação ao corte e consequentemente em relação ao ponto D, são: VB = 17 kN e o 10 kN/m em uma distância de B até o corte, que chamamos de x, portanto temos:
MBD = + 17x – 10x.(x/2) -> MBD = + 17x – 5x²
Em x = 0 -> MBD = + 17.0 – 5.0² -> MBD = 0
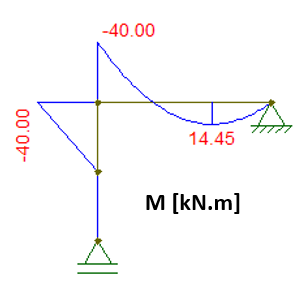
Em x = 1,70 m (Mmax) -> MBD = + 17.1,7 – 5.1,7² -> MBD = + 14,45 kN.m (Tração em baixo)
Em x = 5 m -> MBD = + 17.5 – 5.5² -> MBD = – 40 kN.m (Tração em cima)
Agora que fizemos todos os cálculos, podemos fazer os diagramas:
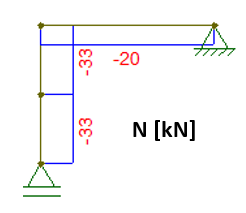
Até a próxima galera! Se tiverem dúvidas em alguma passagem do exercício, deixe – as nos comentários.
A sua dúvida pode ser a mesma de outro aluno!
Abraços!