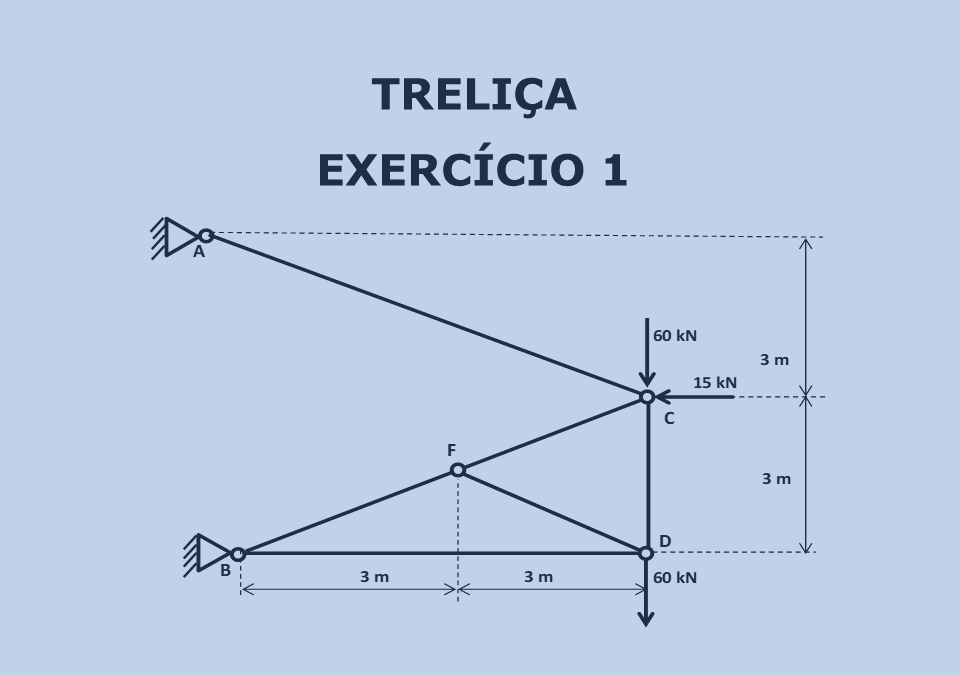
Questão Proposta:
A figura acima representa uma treliça como modelo estrutural de uma construção metálica. Para avaliar a rigidez desta estrutura, determine os valores dos esforços internos em cada barra, indicando se a barra está sendo tracionada ou comprimida.
Para resolver este exercício, precisamos, inicialmente, determinar as reações dos apoios. Posteriormente aplicaremos o método dos nós para determinar cada esforço interno na barra. Então, vamos adotar os seguintes sentidos das reações:
Passo 1) Reações dos apoios

Para determinar as reações dos apoios, vamos adotar os sentidos positivos, ou seja, horizontal para a direita e vertical para cima. Se nossas reações derem negativas, inverteremos os sentidos das mesmas. Para aplicar a somatória dos momentos, vamos adotar o sentido horário negativo. Logo, nosso sistema de referência ficou assim:
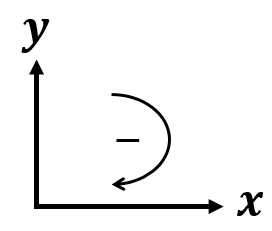
Vamos aplicar a somatória de momento no apoio que tem mais reações, sendo assim, aplicaremos a somatória no apoio B! Mas vejam que temos duas parcelas do RA, uma na horizontal e outra na vertical. Vamos ilustrá-las com um ângulo conhecido.
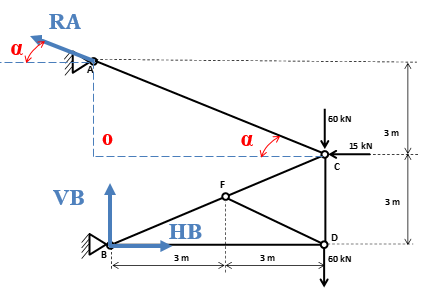
Com o ângulo α localizado na força RA, conseguimos decompô-la e descrever suas componentes em função deste ângulo. Lembrando que a componente horizontal está “com o ângulo α”, portanto cosseno α e a vertical está “sem o ângulo α”, portanto senoα
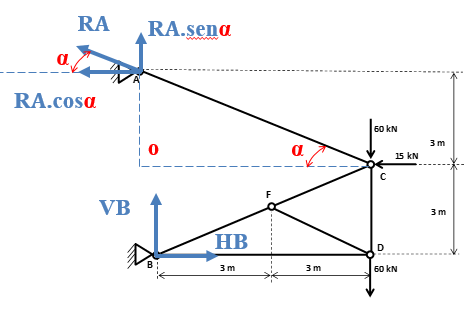
Para facilitar os nossos cálculos, vamos determinar o seno e cosseno do ângulo α. Antes devemos calcular o valor da hipotenusa e posteriormente aplicar as relações trigonométricas. Chamaremos a hipotenusa do triângulo AOC de z. Então temos:
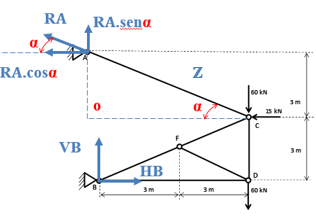

Após realizar a decomposição da força RA, podemos aplicar a somatória de momento no apoio B. Vale ressaltar que a componente RA.sen α não produz momento em relação ao Apoio B, pois esta componente não tem um “braço” perpendicular ao apoio B. Para tanto, apenas a componente horizontal produz momento em relação ao apoio B! Sendo assim, temos:

Vamos, agora, aplicar a somatória de forças verticais para encontrar a reação VB:

Vamos, agora, aplicar a somatória de forças horizontais para encontrar a reação HB:

Passo 2) Análise dos nós
Com as reações dos apoios determinadas, vamos analisar os nós separadamente. Iniciaremos a análise pelo nó A. Adotaremos todas as forças “saindo do nó” e “indo” em direção a barra. Isso significa que estamos supondo tração no nó, sendo assim, se nosso esforço resultar positivo, o esforço é de tração, caso contrário é compressão. Vamos ilustrar a situação:
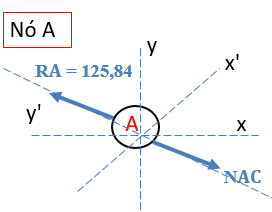
Para não termos que decompor as forças em relação aos eixos x e y, vamos utilizar o eixo y’ para somatórias das forças.

Vamos, então, analisar o nó C.
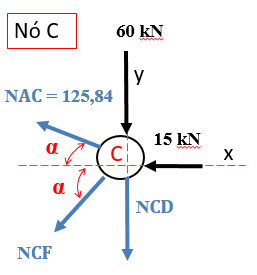
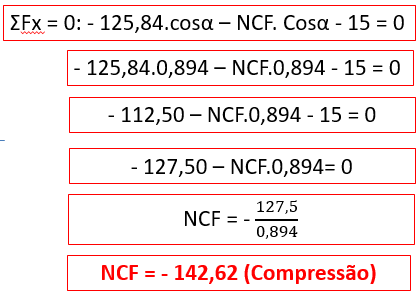
Com a força NCF determinada, podemos aplicar a somatória de forças em relação ao eixo y para determinar a força NCD

Vamos, agora, analisar o nó D.
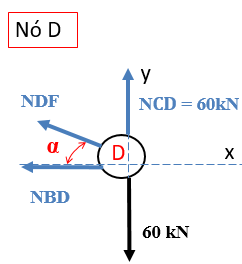
Neste nó, nós temos que colocar o ângulo α com a força inclinada, assim conseguiremos trabalhar com suas componentes. Vamos, então, aplicar a somatória de forças em relação ao eixo y.
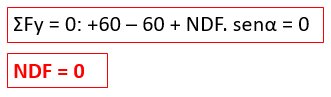
Com a força NDF = 0, podemos aplicar a somatória de forças em relação ao eixo x para determinar a força NBD.

Vamos, agora, analisar o nó F.
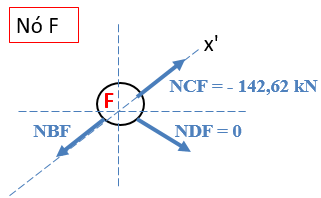
Como a força NDF = 0, podemos aplicar a somatória de forças em relação ao eixo x’ para determinar a força NBF.

Com todas as forças determinadas, podemos dar a resposta solicitada através de uma tabela autoexplicativa.
RESPOSTA
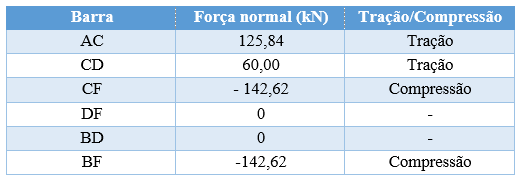
Até a próxima galera! Se tiverem dúvidas em alguma passagem do exercício, deixe – as nos comentários.
A sua dúvida pode ser a mesma de outro aluno!
Abraços!