(Clique aqui e veja a resolução através de um vídeo)
Questão Proposta:
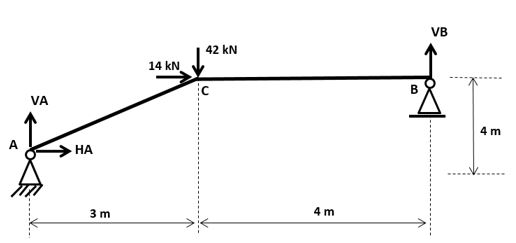
A estrutura ilustrada acima é composta por um único material e contém uma única seção (EI = constante). Determine sua energia considerando apenas flexão.
Vamos, inicialmente, relembrar como nós calculamos a energia por flexão. Sabemos que a fórmula é dada por:
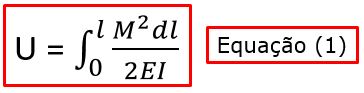
A equação (1) descreve a fórmula genérica da energia por flexão. Ela diz que que a energia é a integral de um momento fletor em relação a um comprimento. Como os momentos fletores em cada trecho são diferentes, vamos desmembrar a equação (1). Ficamos então, com:

Para calcular a energia em cada trecho, devemos determinar o momento e posteriormente elevá-lo ao quadrado. Notem que nesse exercício precisaremos das reações dos apoios para determinar os momentos fletores. Logo, o nosso passo 1 será determinar as reações dos apoios. Para isso, vamos adotar os seguintes sentidos das reações:
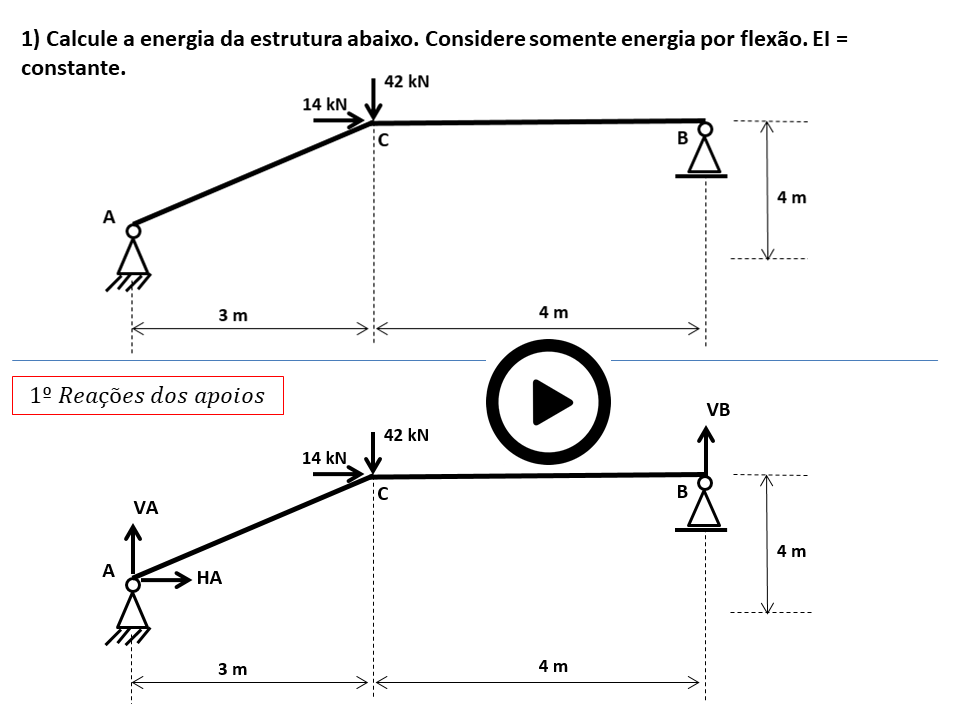
Passo 1) Reações dos apoios
Para determinar as reações dos apoios, vamos adotar os sentidos positivos, ou seja, horizontal para a direita e vertical para cima. Se nossas reações derem negativas, inverteremos os sentidos das mesmas. Para aplicar a soma dos momentos, vamos adotar o sentido horário negativo. Logo, nosso sistema de referência ficou assim:
Vamos aplicar a somatória de momento no apoio que tem mais reações, sendo assim, aplicaremos a somatória no apoio A! Então, teremos:

Vamos agora, aplicar a somatória de forças verticais para encontrar a reação VA:

Vamos, agora, aplicar a somatória de forças horizontais para encontrar a reação HA:

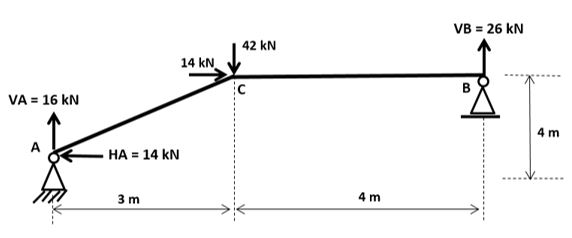
Como a nossa reação HA deu negativa, vamos inverter o sentido inicial adotado e colocar o valor positivo. Ficando assim:
PASSO 2) Análise dos trechos
Com as reações dos apoios determinadas, vamos analisar os trechos separadamente. Vamos iniciar a análise no trecho BC fazendo um corte da direita para a esquerda.
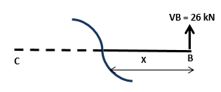
Nesse trecho, vemos que o comportamento do momento é positivo, pois faz a viga sorrir, conforme imagem abaixo:
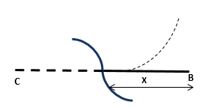
Dessa forma a nossa equação terá o sinal positivo. Resultando em:
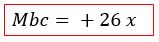
Lembrando que nós queremos a função do quadrado do momento, e não a função do momento. Para tanto, vamos elevar a nossa função ao quadrado.

Vamos, agora, aplicar a nossa equação do momento na equação (1). Teremos:

Note que o nosso dl passou a ser dx, pois estamos integrando em relação ao eixo x. Vamos, então, integrar a função.
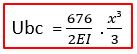
Lembrando que nossos limites de integração vão de x = 0 até x = 4. Vamos, agora, substituir os limites de integração.

Vamos, então, analisar o trecho AC. Este está no eixo x’. Vamos iniciar a análise deste trecho fazendo um corte da esquerda para a direita.
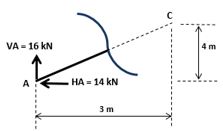
Nota – se que as forças não estão no eixo x’, para tanto vamos identificar um ângulo conhecido para decompô-las.
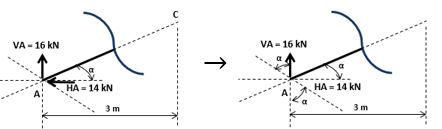
Com o ângulo α junto as forças, podemos iniciar o processo de decomposição:
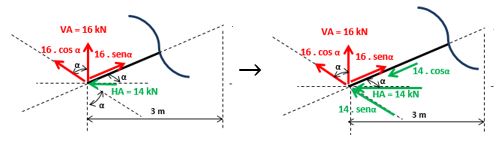
Mas quanto vale o seno e o cosseno de α?
Aplicando as funções trigonométricas no triângulo formado pelo trecho AC, temos:
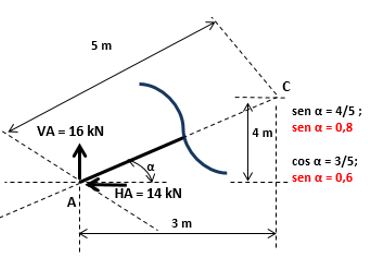
Voltemos a decomposição dos esforços:
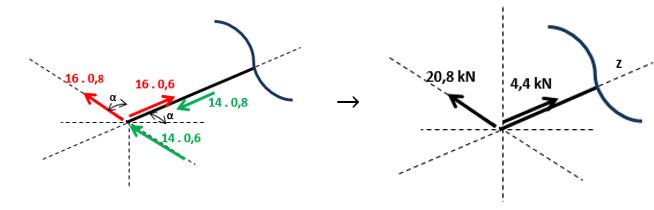
Na figura final, notamos que a única parcela que produz momento em relação ao nosso corte é o 20,8 kN. O Momento produzido por ele terá o valor positivo pois faz a nossa viga “sorrir”. Veja:
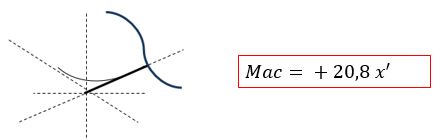
Lembrando que nós queremos a função do quadrado do momento, e não a função do momento. Para tanto, vamos elevar a nossa função ao quadrado.
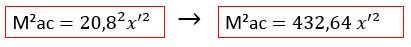
Vamos, agora, aplicar a nossa equação do momento na equação (1). Teremos:

Note que o nosso dl passou a ser dx’, pois estamos integrando em relação ao eixo inclinado x’. Vamos, então, integrar a função.
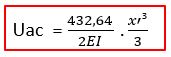
Lembrando que nossos limites de integração vão de x’ = 0 até x’ = 5. Vamos, agora, substituir os limites de integração.

Com isso, a energia total do sistema é:
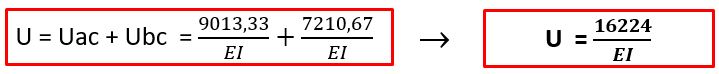
Até a próxima galera! Se tiverem dúvidas em alguma passagem do exercício, deixe – as nos comentários.
A sua dúvida pode ser a mesma de outro aluno!
Abraços!